General
- Details
- Parent Category: Math League Website
6th, 7th, and 8th Grade Contests
Math League's 6th, 7th, and 8th grade contests challenge students and schools in interschool league competitions. Students in each league compete for the highest scores, while schools compete for the highest team score: the total of the top 5 scores in each school. Each contest's questions cover material appropriate to each grade level. Questions may cover: basic topics, plus exponents, fractions, reciprocals, decimals, rates, ratios, percents, angle measurement, perimeter, area, circumference, basic roots, patterns, sequences, integers, triangles and right triangles, and other topics, depending on the grade level. Detailed solution sheets demonstrate the methods used to solve each problem. These contests encourage a variety of problem-solving skills and methods, to improve students' abilities and understanding of mathematical connections, while having fun! Contest Format: Each contest consists of 35 multiple-choice questions that you can do in 30 minutes. On each 3-page contest, the questions on the 1st page are generally straightforward, those on the 2nd page are moderate in difficulty, and those on the 3rd page are more difficult. There is a 6th Grade Score Report, and a 7th and 8th Grade Score Report sent to schools in each league after the contest. |
- Details
- Parent Category: Math League Website
High School ContestsMath League's High School Contests are the best in high school mathematics competition. Students in each league compete for the highest scores, while schools compete for the highest team score: the total of the top 5 scores in each school. These contests consist of 6 High School Contests each year, with 6 questions per contest. There are 6 score reports per year for each league, showing each participating school's team scores, high scoring schools and students, and students with a perfect score. Each score report is accompanied by a newsletter, which includes comments and alternate solutions from teachers and students. All high school students in accredited schools are welcome to compete. Problems draw from a wide range of high school topics: geometry, algebra, trigonometry, logarithms, series, sequences, exponents, roots, integers, real numbers, combinations, probability, coordinate geometry, and more. No knowledge of calculus is required to solve any of these problems. Detailed solution sheets demonstrate the methods used to solve each problem, including various approaches where appropriate. Working through these problems and our contest problem books is excellent practice for the SAT and college-bound students. Contest Format: There are 6 High School Contests each year, with 6 questions per contest. There is a 30 minute time limit for each contest. On each contest, the last two questions are generally more difficult than the first four. The final question on each contest is intended to challenge the very best mathematics students. The problems require no knowledge beyond secondary school mathematics. No knowledge of calculus is required to solve any of these problems. Two to four of the questions on each contest only require a knowledge of elementary algebra. Starting with the 1992-93 school year, students have been permitted to use any calculator on any of our contests. |
| Sample 05-06 High School Contest & Solutions (PDF) Dates / Fees • Register Online • Print Order Form Score Reports • Rules • FAQ • Check School Registration |
2010-2011 High School Contest Dates | |
|---|---|
| Contest # | Official Date* (Tuesdays) |
| HS Contest 1 HS Contest 2 HS Contest 3 HS Contest 4 HS Contest 5 HS Contest 6 | October 19, 2010 November 16, 2010 December 14, 2010 Janaury 11, 2011 February 22, 2011 March 22, 2011 |
*Alternate contest dates may be scheduled one week before the contest dates, in the event of scheduling conflicts. | |
- Details
- Parent Category: Math League Website
Positive and negative numbers
About positive and negative numbers
The number line
Absolute value of positive and negative numbers
Adding positive and negative numbers
Subtracting positive and negative numbers
Multiplying positive and negative numbers
Dividing positive and negative numbers
Coordinates
Comparing positive and negative numbers
Reciprocals of negative numbers
About Positive and Negative Numbers
Positive numbers are any numbers greater than zero, for example: 1, 2.9, 3.14159, 40000, and 0.0005. For each positive number, there is a negative number that is its opposite. We write the opposite of a positive number with a negative or minus sign in front of the number, and call these numbers negative numbers. The opposites of the numbers in the list above would be: -1, -2.9, -3.14159, -40000, and -0.0005. Negative numbers are less than zero (see the number line for a more complete explanation of this). Similarly, the opposite of any negative number is a positive number. For example, the opposite of -12.3 is 12.3.
We do not consider zero to be a positive or negative number.
The sum of any number and its opposite is 0.
The sign of a number refers to whether the number is positive or negative, for example, the sign of -3.2 is negative, and the sign of 442 is positive.
We may also write positive and negative numbers as fractions or mixed numbers.
The following fractions are all equal:
(-1)/3, 1/(-3), -(1/3) and - 1/3.
The following mixed numbers are all equal:
-1 1/6, -(1 1/6), (-7)/6, 7/(-6), and - 7/6.
The Number Line
The number line is a line labeled with positive and negative numbers in increasing order from left to right, that extends in both directions. The number line shown below is just a small piece of the number line from -4 to 4.
For any two different places on the number line, the number on the right is greater than the number on the left.
Examples:
4 > -2, 1 > -0.5, -2 > -4, and 0 > -15
Absolute Value of Positive and Negative Numbers
The number of units a number is from zero on the number line. The absolute value of a number is always a positive number (or zero). We specify the absolute value of a number n by writing n in between two vertical bars: |n|.
Examples:
|6| = 6
|-0.004| = 0.004
|0| = 0
|3.44| = 3.44
|-3.44| = 3.44
|-10000.9| = 10000.9
Adding Positive and Negative Numbers
1) When adding numbers of the same sign, we add their absolute values, and give the result the same sign.
Examples:
2 + 5.7 = 7.7
(-7.3) + (-2.1) = -(7.3 + 2.1) = -9.4
(-100) + (-0.05) = -(100 + 0.05) = -100.05
2) When adding numbers of the opposite signs, we take their absolute values, subtract the smaller from the larger, and give the result the sign of the number with the larger absolute value.
Example:
7 + (-3.4) = ?
The absolute values of 7 and -3.4 are 7 and 3.4. Subtracting the smaller from the larger gives 7 - 3.4 = 3.6, and since the larger absolute value was 7, we give the result the same sign as 7, so 7 + (-3.4) = 3.6.
Example:
8.5 + (-17) = ?
The absolute values of 8.5 and -17 are 8.5 and 17. Subtracting the smaller from the larger gives 17 - 8.5 = 8.5, and since the larger absolute value was 17, we give the result the same sign as -17, so 8.5 + (-17) = -8.5.
Example:
-2.2 + 1.1 = ?
The absolute values of -2.2 and 1.1 are 2.2 and 1.1. Subtracting the smaller from the larger gives 2.2 - 1.1 = 1.1, and since the larger absolute value was 2.2, we give the result the same sign as -2.2, so -2.2 + 1.1 = -1.1.
Example:
6.93 + (-6.93) = ?
The absolute values of 6.93 and -6.93 are 6.93 and 6.93. Subtracting the smaller from the larger gives 6.93 - 6.93 = 0. The sign in this case does not matter, since 0 and -0 are the same. Note that 6.93 and -6.93 are opposite numbers. All opposite numbers have this property that their sum is equal to zero. Two numbers that add up to zero are also called additive inverses.
Subtracting Positive and Negative Numbers
Subtracting a number is the same as adding its opposite.
Examples:
In the following examples, we convert the subtracted number to its opposite, and add the two numbers.
7 - 4.4 = 7 + (-4.4) = 2.6
22.7 - (-5) = 22.7 + (5) = 27.7
-8.9 - 1.7 = -8.9 + (-1.7) = -10.6
-6 - (-100.6) = -6 + (100.6) = 94.6
Note that the result of subtracting two numbers can be positive or negative, or 0.
Multiplying Positive and Negative Numbers
To multiply a pair of numbers if both numbers have the same sign, their product is the product of their absolute values (their product is positive). If the numbers have opposite signs, their product is the opposite of the product of their absolute values (their product is negative). If one or both of the numbers is 0, the product is 0.
Examples:
In the product below, both numbers are positive, so we just take their product.
0.5 × 3 = 1.5
In the product below, both numbers are negative, so we take the product of their absolute values.
(-1.1) × (-5) = |-1.1| × |-5| = 1.1 × 5 = 5.5
In the product of (-3) × 0.7, the first number is negative and the second is positive, so we take the product of their absolute values, which is |-3| × |0.7| = 3 × 0.7 = 2.1, and give this result a negative sign: -2.1, so (-3) × 0.7 = -2.1
In the product of 21 × (-3.1), the first number is positive and the second is negative, so we take the product of their absolute values, which is |21| × |-3.1| = 21 × 3.1 = 65.1, and give this result a negative sign: -65.1, so 21 × (-3.1) = -65.1.
To multiply any number of numbers:
1. Count the number of negative numbers in the product.
2. Take the product of their absolute values.
3. If the number of negative numbers counted in step 1 is even, the product is just the product from step 2, if the number of negative numbers is odd, the product is the opposite of the product in step 2 (give the product in step 2 a negative sign). If any of the numbers in the product is 0, the product is 0.
Example:
2 × (-1.1) × 5 (-1.2) × (-9) = ?
Counting the number of negative numbers in the product, we see that there are 3 negative numbers: -1.1, -1.2, and -9. Next, we take the product of the absolute values of each number: 2 × |-1.1| × 5 × |-1.2| × |-9| = 2 × 1.1 × 5 × 1.2 × 9 = 118.8
Since there were an odd number of numbers, the product is the opposite of 118.8, which is -118.8, so 2 × (-1.1) × 5 (-1.2) × (-9) = -118.8.
Dividing Positive and Negative Numbers
To divide a pair of numbers if both numbers have the same sign, divide the absolute value of the first number by the absolute value of the second number.
To divide a pair of numbers if both numbers have different signs, divide the absolute value of the first number by the absolute value of the second number, and give this result a negative sign.
Examples:
In the division below, both numbers are positive, so we just divide as usual.
7 ÷ 2 = 3.5
In the division below, both numbers are negative, so we divide the absolute value of the first by the absolute value of the second.
(-2.4) ÷ (-3) = |-2.4| ÷ |-3| = 2.4 ÷ 3 = 0.8
In the division (-1) ÷ 2.5, both number have different signs, so we divide the absolute value of the first number by the absolute value of the second, which is |-1| ÷ |2.5| = 1 ÷ 2.5 = 0.4, and give this result a negative sign: -0.4, so (-1) ÷ 2.5 = -0.4.
In the division 9.8 ÷ (-0.7), both number have different signs, so we divide the absolute value of the first number by the absolute value of the second, which is |9.8| ÷ |-0.7| = 9.8 ÷ 0.7 = 14, and give this result a negative sign: -14, so 9.8 ÷ (-0.7) = -14.
Coordinates
Number coordinates are pairs of numbers that are used to determine points in a grid, relative to a special point called the origin. The origin has coordinates (0,0). We can think of the origin as the center of the grid or the starting point for finding all other points. Any other point in the grid has a pair of coordinates (x,y). The x value or x-coordinate tells how many steps left or right the point is from the point (0,0), just like on the number line (negative is left of the origin, positive is right of the origin). The y value or y-coordinate tells how many steps up or down the point is from the point (0,0), (negative is down from the origin, positive is up from the origin). Using coordinates, we may give the location of any point in the grid we like by simply using a pair of numbers.
Example:
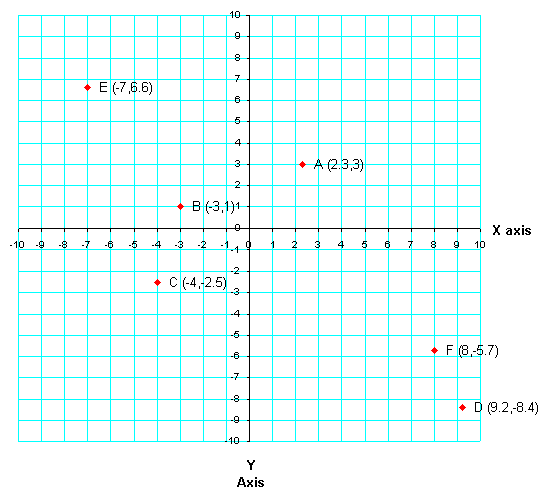
The origin below is where the x-axis and the y-axis meet. Point A has coordinates (2.3,3), since it is 2.3 units to the right and 3 units up from the origin. Point B has coordinates (-3,1), since it is 3 units to the left, and 1 unit up from the origin. Point C has coordinates (-4,-2.5), since it is 4 units to the left, and 2.5 units down from the origin. Point D has coordinates (9.2,-8.4); it is 9 units to the right, and 8.4 units down from the origin. Point E has coordinates (-7,6.6); it is 7 units to the left, and 6.6 units up from the origin. Point F has coordinates (8,-5.7); it is 8 units to the right, and 5.7 units down from the origin.
Comparing Positive and Negative Numbers
We can compare two different numbers by looking at their positions on the number line. For any two different places on the number line, the number on the right is greater than the number on the left. Note that every positive number is greater than any negative number.
Examples:
9.1 > 4, 6 > -9.3, -2 > -8, and 0 > -5.5
-2 < -13, -1 < -0.5, -7 < -5, and -10 < 0.1
Reciprocals of Negative Numbers
The reciprocal of a positive or negative fraction is obtained by switching its numerator and denominator, the sign of the new fraction remains the same. To find the reciprocal of a mixed number, first convert the mixed number to an improper fraction, then switch the numerator and denominator of the improper fraction. Notice that when you multiply negative fractions with their reciprocals, the product is always 1 (NOT -1).
Examples:
What is the reciprocal of -2/7? We just switch the numerator and denominator, and keep the same sign: -7/2.
What is the reciprocal of - 5 1/8? First, we convert to a negative improper fraction: -5 1/8 = - 41/8, then we switch the numerator and denominator, and keep the same sign: - 8/41.
- Details
- Parent Category: Math League Website
Introduction to Algebra
Variables Expressions
Equations
Solution of an equation
Simplifying equations
Combining like terms
Simplifying with addition and subtraction
Simplifying by multiplication
Simplifying by division
Word problems as equations
Sequences
Variables
A variable is a symbol that represents a number. Usually we use letters such as n, t, or x for variables. For example, we might say that s stands for the side-length of a square. We now treat s as if it were a number we could use. The perimeter of the square is given by 4 × s. The area of the square is given by s× s. When working with variables, it can be helpful to use a letter that will remind you of what the variable stands for: let n be the number of people in a movie theater; let t be the time it takes to travel somewhere; let d be the distance from my house to the park.Expressions
An expression is a mathematical statement that may use numbers, variables, or both.Example:
The following are examples of expressions:
2
x
3 + 7
2 × y + 5
2 + 6 × (4 - 2)
z + 3 × (8 - z)
Example:
Roland weighs 70 kilograms, and Mark weighs k kilograms. Write an expression for their combined weight. The combined weight in kilograms of these two people is the sum of their weights, which is 70 + k.
Example:
A car travels down the freeway at 55 kilometers per hour. Write an expression for the distance the car will have traveled after h hours. Distance equals rate times time, so the distance traveled is equal to 55 × h..
Example:
There are 2000 liters of water in a swimming pool. Water is filling the pool at the rate of 100 liters per minute. Write an expression for the amount of water, in liters, in the swimming pool after m minutes. The amount of water added to the pool after m minutes will be 100 liters per minute times m, or 100 × m. Since we started with 2000 liters of water in the pool, we add this to the amount of water added to the pool to get the expression 100 × m + 2000.
To evaluate an expression at some number means we replace a variable in an expression with the number, and simplify the expression.
Example:
Evaluate the expression 4 × z + 12 when z = 15.
We replace each occurrence of z with the number 15, and simplify using the usual rules: parentheses first, then exponents, multiplication and division, then addition and subtraction.
4 × z + 12 becomes
4 × 15 + 12 =
60 + 12 =
72
Example:
Evaluate the expression (1 + z) × 2 + 12 ÷ 3 - z when z = 4.
We replace each occurrence of z with the number 4, and simplify using the usual rules: parentheses first, then exponents, multiplication and division, then addition and subtraction.
(1 + z) × 2 + 12 ÷ 3 - z becomes
(1 + 4) × 2 + 12 ÷ 3 - 4 =
5 × 2 + 12 ÷ 3 - 4 =
10 + 4 - 4 =
10.
Equations
An equation is a statement that two numbers or expressions are equal. Equations are useful for relating variables and numbers. Many word problems can easily be written down as equations with a little practice. Many simple rules exist for simplifying equations.Example:
The following are examples of equations:
2 = 2
17 = 2 + 15
x = 7
7 = x
t + 3 = 8
3 × n +12 = 100
w + 4 = 12 - w
y - 1 - 2 - 9.3 = 34
3 × (d + 4) - 11 = 321 - 23
Example:
Translate the following word problem into an equation:
My age in years y plus 20 is equal to four times my age, minus 10.
The first expression stands for "my age in years plus 20", which is y + 20.
This is equal to the second expression for "four times my age, minus 10", which is 4 × y - 10.
Setting these two expressions equal to one another gives us the equation:
y + 20 = 4 × y - 10
Solution of an Equation
When an equation has a variable, the solution to the equation is the number that makes the equation true when we replace the variable with its value.Example:
We say y = 3 is a solution to the equation 4 × y + 7 = 19, for replacing each occurrence of y with 3 gives us
4 × 3 + 7 = 19 ==>
12 + 7 = 19 ==>
19 = 19 which is true.
Examples:
x = 100 is a solution to the equation x ÷ 2 - 40 = 10
z = 12 is a solution to the equation 5 × (z - 6) = 30
Counterexample:
y = 10 is NOT a solution to the equation 4 × y + 7 = 19. When we replace each y with 10, we get
4 × 10 + 7 = 19 ==>
40 + 7 = 19 ==>
47 = 19 not true!
Counterexamples:
x = 200 is NOT a solution to the equation x ÷ 2 - 40 = 10
z = 20 is NOT a solution to the equation 5 × (z - 6) = 30
Simplifying Equations
To find a solution for an equation, we can use the basic rules of simplifying equations. These are as follows:1) You may evaluate any parentheses, exponents, multiplications, divisions, additions, and subtractions in the usual order of operations. When evaluating expressions, be careful to use the associative and distributive properties properly.
2) You may combine like terms. This means adding or subtracting variables of the same kind. The expression 2x + 4x simplifies to 6x. The expression 13 - 7 + 3 simplifies to 9.
3) You may add any value to both sides of the equation.
4) You may subtract any value from both sides of the equation. This is best done by adding a negative value to each side of the equation.
5) You may multiply both sides of the equation by any number except 0.
6) You may divide both sides of the equation by any number except 0.
Hint: Since subtracting any number is the same as adding its negative, it can be helpful to replace subtractions with additions of a negative number.
Example:
This problem illustrates grouping like terms and dealing with subtraction in an equation.
Solve x - 12 + 20 = 37.
Replacing the -12 with a +(-12), we get
x + (-12) + 20 = 37.
Since addition is associative, the two like terms (the integers) may be combined.
(12) + 20 = 8
The left side of the equation becomes
x + 8 = 37.
Now we may subtract 8 from each side of the equation, (we will actually add a -8 to each side).
x + 8 + (-8) = 37 + (-8)
x + 0 = 29
x = 29
We can check this solution in the original equation:
29 - 12 + 20 = 37x + 0 = 29
17 + 20 = 37
37 = 37 so our solution is correct.
Example:
This problem illustrates the proper use of the distributive property.
Solve 2 × (x + 1 + 4) = 20.
Grouping like terms in the parentheses, the left side of the equation becomes
2 × (x + 1 + 4) ==> 2 × (x + 5).
Using the distributive property,
2 × (x + 5) ==> 2 × x + 2 × 5.
Carrying out multiplications,
2 × x + 2 × 5 ==> to 2x + 10.
The equation now becomes
2x + 10 = 20.
Subtracting a 10 (adding a -10) to each side gives us
2x + 10 + (-10) = 20 + (-10) ==>
2x + (10 + (-10)) = 20 - 10 ==>
2x + 0 = 10 ==>
2x = 10.
Since the x is multiplied by 2, we divide both sides by 2 to solve for x:
2x = 10 ==>
2x ÷ 2 = 10 ÷ 2 ==>
(2x)/2 = 5 ==>
x = 5.
We can check this solution in the original equation:
2 × (5 + 1 + 4) = 20 ==>
2 × 10 = 20 ==>
20 = 20 so our solution is correct.
Combining like terms
One of the most common ways to simplify an expression is to combine like terms. Numeric terms may be combined, and any terms with the same variable part may be combined.Example:
Consider the expression 2 + 7x + 12 - 3x - 5. The numeric like terms are the numbers 2, 12, and 5. The variable like terms are 7x and 3x. Combining the numeric like terms, we have 2 + 12 - 5 = 14 - 5 = 9. Combining the variable like terms, we have 7x - 3x = 4x, so the expression 2 + 7x + 12 - 3x - 5 simplifies to 9 + 4x.
Simplifying with addition and subtraction
We can use addition and subtraction to get all the terms with variables on one side of an equation, and all the numeric terms on the other.The equations 3x = 17, 21 = y, and z/12 = 24 each have a variable term on one side of the = sign, and a number on the other.
The equations x + 3 = 12, 21 = 30 - y, and (z + 2) × 4 = 10 do not.
We usually do this after simplifying each side using the distributive rules, eliminating parentheses, and combining like terms. Since addition is associative, it can be helpful to add a negative number to each side instead of subtracting to avoid mistakes.
Examples:
For the equation 3x + 4 = 12, we can isolate the variable term on the left by subtracting a 4 from both sides:
3x + 4 - 4 = 12 - 4 ==>
3x = 8.
For the equation 7y - 200 = 10, subtracting the 200 on the left side is the same as adding a -200:
7y + (-200) = 10.
If we add 200 to both sides of the equation, the 200 and -200 will cancel each other:
7y + (-200) + 200 = 10 + 200 ==>
7y = 210.
For the equation 8 = 20 - z, we can add z to both sides to get 8 + z = 20 - z + z ==> 8 + z = 20. Now subtracting 8 from both sides,
8 + z - 8 = 20 - 8 ==>
z = 12, so we get a solution for z.
Simplfying by multiplication
When solving for a variable, we want to get a solution like x = 3 or z = 2001. When a variable is divided by some number, we can use multiplication on both sides to solve for the variable.Example:
Solve for x in the equation x ÷ 12 = 5.
Since the x on the left side is being divided by 12, the equation is the same as x × 1/12 = 5. Multiplying both sides by 12 will cancel the 1/12 on the left side:
x × 1/12 × 12 = 5 × 12 ==>
x × 1 = 60 ==>
x = 60.
Simplifying by division
When solving for a variable, we want to get a solution like x = 3 or z = 2001. When a variable is multiplied by some number, we can use division on both sides to solve for the variable.Example:
Solve for x in the equation 7x = 133. Since the x on the left side is being multiplied by 7, we can divide both sides by 7 to solve for x:
7x ÷ 7 = 133 ÷ 7 ==>
(7x)/7 = 133 ÷ 7 ==>
x/1 = 19 ==>
x = 19.
Note that dividing by 7 is the same as multiplying both sides by 1/7.
Word problems as equations
When converting word problems to equations, certain "key" words tell you what kind of operations to use: addition, multiplication, subtraction, and division. The table below shows some common phrases and the operation to use.| Word | Operation | Example | As an equation |
| sum | addition | The sum of my age and 10 equals 27. | y + 10 = 27 |
| difference | subtraction | The difference between my age and my younger sister's age, who is 11 years old, is 5 years. | y - 11 = 5 |
| product | multiplication | The product of my age and 14 is 168. | y × 14 = 168 |
| times | multiplication | Three times my age is 60. | 3 × y = 60 |
| less than | subtraction | Seven less than my age equals 32. | y - 7 = 32 |
| total | addition | The total of my pocket change and 20 dollars is $22.43. | y + 20 = 22.43 |
| more than | addition | Eleven more than my age equals 43. | 11 + y = 43 |
Sequences
A sequence is a list of items. We can specify any item in the list by its place in the list: first, second, third, fourth, and so on. Many useful lists have patterns so we know what items occur in each place in the list. There are 2 kinds of sequences. A finite sequence is a list made up of a finite number of items. An infinite sequence is a list that continues without end.Examples:
The following are examples of finite sequences.
The sequence 1, 3, 5, 7, 9, 11, 13, 15, 17, 19 is the sequence of the first 10 odd numbers.
The sequence a, e, i, o, u, is the sequence of vowels in the alphabet.
The sequence m, m, m, m, m, m is the sequence of 6 m's.
The sequence 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0 is the sequence of 12 alternating 1's and 0's.
The sequence 1, 2, 3, 4, ..., 9998, 9999, 10000 is the sequence of the first ten thousand integers.
The sequence 0, 1, 4, 9, 16, 25, 36, 49 is the sequence of the squares of the first 8 whole numbers.
Examples:
The following are examples of infinite sequences.
The sequence 2, 4, 6, 8, 10, 12, 14, 16, ... is the sequence of even whole numbers. The 100th place in this sequence is the number 200.
The sequence a, b, c, a, b, c, a, b, c, a, b, ... is the sequence of the letters a, b, c, repeating in this pattern forever.
The 100th place in this sequence is the letter a. The 300th place in this sequence is the letter c.
The sequence -1, 2, -3, 4, -5, 6, -7, 8, -9, ... is the sequence of integers with alternating signs. The 10th place in this sequence is 10. The 100th place in this sequence is 100. The 101st place in this sequence is -101.
The sequence 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, ... is a sequence of 1's separated by 1 zero, then 2 zeros, then 3 zeros, and so on. The 100th place in this sequence is a 0. The 105th place in this sequence is a 1.
The sequence 1, 3, 6, 10, 15, 21, 28, 36, 45, ... is the sequence of places the 1 occurs in the sequence of 1's and 0's above! If this sequence seems strange, note the difference between pairs of numbers next to one another:
3 - 1 = 2
6 - 3 = 3
10 - 6 = 4
15 - 10 = 5
21 - 15 = 6
28 - 21 = 7
Checking these differences makes the pattern clearer.
1, 1, 1, 1, 1, 1, ... is the sequence where every item in the list is the number 1.
1, 2, 3, 4, 5, 6, 7, ... is the sequence of counting numbers. Each item in the list is its place number in the list.
a, b, a, b, a, b, a, b, ... is the sequence of alternating letters a and b. The a's occur in odd-numbered places, and the b's occur in the even-numbered places.
1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, ... is the sequence of reciprocals of the whole numbers.
1, 4, 9, 16, 25, 36, 49, 64, 81, ... is the sequence of squares of the whole numbers.
a, e, i, o, u, a, e, i, o, u, a, e, ... is the repeating sequence of vowels in the alphabet.
4, 7, 10, 13, 16, 19, 22, 25, ... is the sequence of numbers beginning with the number 4, and each number in the list is 3 more than the number before it.
- Details
- Parent Category: Math League Website
Length The standard unit of length in the metric system is the meter. Other units of length and their equivalents in meters are as follows: We abbreviate these lengths as follows: For reference, 1 meter is a little longer than 1 yard or 3 feet. It is about half the height of a very tall adult. A centimeter is nearly the diameter of a dime, a little less than half an inch. A millimeter is about the thickness of a dime.Metric units and Measurement
Volume
Mass
Time
Temperature
Decimals in measurement
Length
1 millimeter = 0.001 meter
1 centimeter = 0.01 meter
1 decimeter = 0.1 meter
1 kilometer = 1000 meters
1 millimeter = 1 mm
1 centimeter = 1 cm
1 meter = 1 m
1 decimeter = 1 dm
1 kilometer = 1 km
The standard unit of volume in the metric system is the liter. One liter is equal to 1000 cubic centimeters in volume. Other units of volume and their equivalents in liters are as follows: From these units, we see that 1000 milliliters equal 1 liter; so 1 milliliter equals 1 cubic centimeter in volume. We abbreviate these volumes as follows: For reference, 1 liter is a little more than 1 quart. One teaspoon equals about 5 milliliters. The standard unit of mass in the metric system is the gram. Other units of mass and their equivalents in grams are as follows: We abbreviate these masses as follows: For reference, 1 gram is about the mass of a paper clip. One kilogram is about the mass of a liter of water. The following conversions are useful when working with time: In practice, every three calendar years will have 365 days, and every fourth year is a "leap year", which has 366 days, to make up for the extra quarter day over four years. The years 1992, 1996, 2000, and 2004 are all leap years. This gives us a total of 52 complete 7 day weeks in each calendar year, with 1 day left over (or 2 in a leap year). The year is divided into 12 months, each of which has 30 or 31 days, except for February, which has 28 days (or 29 days in a leap year). Temperature is expressed in degrees Celsius in the metric system. The boiling point of water (at sea level) is 100°Celsius, or 100°C. The freezing point of water (at sea level) is 0° Celsius. A hot day is about 30° Celsius.
Volume
1 milliliter = 0.001 liter
1 centiliter = 0.01 liter
1 deciliter = 0.1 liter
1 kiloliter = 1000 liters
1 milliliter = 1 ml
1 centiliter = 1 cl
1 deciliter = 1 dl
1 liter = 1 l
1 kiloliter = 1 kl
Mass
1 milligram = 0.001 gram
1 centigram = 0.01 gram
1 decigram = 0.1 gram
1 kilogram = 1000 grams
1 milligram = 1 mg
1 centigram = 1 cg
1 decigram = 1 dg
1 gram = 1 g
1 kilogram = 1 kg
Time
1 minute = 60 seconds
1 hour = 60 minutes = 3600 seconds
1 day = 24 hours
1 week = 7 days
1 year = 365 1/4 days (for the Earth to travel once around the sun)
Temperature
We use decimals to specify units of measurement when we need more precision about length, volume, mass, or time. For example, when specifying the height of a person 1.63 meters tall, to say that person is 1 or 2 meters tall doesn't give us a very good idea of how tall that person really is.
Decimals in measurement
The prefixes for the different units of length, volume, and mass in the metric system obey the following rules:
| Prefix | Multiply by |
| milli- | 0.001 |
| centi- | 0.01 |
| deci- | 0.1 |
| deka- | 10 |
| hecto- | 100 |
| kilo- | 1000 |
So for example:
1 hectometer = 100 meters
1 centigram = 0.01 gram
3 milliliters = 3 × (0.001 liters) = 0.003 liters
0.9 kilometers = 0.9 × (1000 meters) = 900 meters
- Details
- Parent Category: Math League Website
Integers
Positive and negative integers
The number line
Absolute value of an integer
Adding integers
Subtracting integers
Multiplying integers
Dividing integers
Integer coordinates
Comparing integers
Positive and Negative Integers
Positive integers are all the whole numbers greater than zero: 1, 2, 3, 4, 5, ... . Negative integers are all the opposites of these whole numbers: -1, -2, -3, -4, -5, …. We do not consider zero to be a positive or negative number. For each positive integer, there is a negative integer, and these integers are called opposites. For example, -3 is the opposite of 3, -21 is the opposite of 21, and 8 is the opposite of -8. If an integer is greater than zero, we say that its sign is positive. If an integer is less than zero, we say that its sign is negative.
Example:
Integers are useful in comparing a direction associated with certain events. Suppose I take five steps forwards: this could be viewed as a positive 5. If instead, I take 8 steps backwards, we might consider this a -8. Temperature is another way negative numbers are used. On a cold day, the temperature might be 10 degrees below zero Celsius, or -10°C.
The Number Line
The number line is a line labeled with the integers in increasing order from left to right, that extends in both directions:
For any two different places on the number line, the integer on the right is greater than the integer on the left.
Examples:
9 > 4, 6 > -9, -2 > -8, and 0 > -5
Absolute Value of an Integer
The number of units a number is from zero on the number line. The absolute value of a number is always a positive number (or zero). We specify the absolute value of a number n by writing n in between two vertical bars: |n|.
Examples:
|6| = 6
|-12| = 12
|0| = 0
|1234| = 1234
|-1234| = 1234
Adding Integers
1) When adding integers of the same sign, we add their absolute values, and give the result the same sign.
Examples:
2 + 5 = 7
(-7) + (-2) = -(7 + 2) = -9
(-80) + (-34) = -(80 + 34) = -114
2) When adding integers of the opposite signs, we take their absolute values, subtract the smaller from the larger, and give the result the sign of the integer with the larger absolute value.
Example:
8 + (-3) = ?
The absolute values of 8 and -3 are 8 and 3. Subtracting the smaller from the larger gives 8 - 3 = 5, and since the larger absolute value was 8, we give the result the same sign as 8, so 8 + (-3) = 5.
Example:
8 + (-17) = ?
The absolute values of 8 and -17 are 8 and 17.
Subtracting the smaller from the larger gives 17 - 8 = 9, and since the larger absolute value was 17, we give the result the same sign as -17, so 8 + (-17) = -9.
Example:
-22 + 11 = ?
The absolute values of -22 and 11 are 22 and 11. Subtracting the smaller from the larger gives 22 - 11 = 11, and since the larger absolute value was 22, we give the result the same sign as -22, so -22 + 11 = -11.
Example:
53 + (-53) = ?
The absolute values of 53 and -53 are 53 and 53. Subtracting the smaller from the larger gives 53 - 53 =0. The sign in this case does not matter, since 0 and -0 are the same. Note that 53 and -53 are opposite integers. All opposite integers have this property that their sum is equal to zero. Two integers that add up to zero are also called additive inverses.
Subtracting Integers
Subtracting an integer is the same as adding its opposite.
Examples:
In the following examples, we convert the subtracted integer to its opposite, and add the two integers.
7 - 4 = 7 + (-4) = 3
12 - (-5) = 12 + (5) = 17
-8 - 7 = -8 + (-7) = -15
-22 - (-40) = -22 + (40) = 18
Note that the result of subtracting two integers could be positive or negative.
Multiplying Integers
To multiply a pair of integers if both numbers have the same sign, their product is the product of their absolute values (their product is positive). If the numbers have opposite signs, their product is the opposite of the product of their absolute values (their product is negative). If one or both of the integers is 0, the product is 0.
Examples:
In the product below, both numbers are positive, so we just take their product.
4 × 3 = 12
In the product below, both numbers are negative, so we take the product of their absolute values.
(-4) × (-5) = |-4| × |-5| = 4 × 5 = 20
In the product of (-7) × 6, the first number is negative and the second is positive, so we take the product of their absolute values, which is |-7| × |6| = 7 × 6 = 42, and give this result a negative sign: -42, so (-7) × 6 = -42.
In the product of 12 × (-2), the first number is positive and the second is negative, so we take the product of their absolute values, which is |12| × |-2| = 12 × 2 = 24, and give this result a negative sign: -24, so 12 × (-2) = -24.
To multiply any number of integers:
1. Count the number of negative numbers in the product.
2. Take the product of their absolute values.
3. If the number of negative integers counted in step 1 is even, the product is just the product from step 2, if the number of negative integers is odd, the product is the opposite of the product in step 2 (give the product in step 2 a negative sign). If any of the integers in the product is 0, the product is 0.
Example:
4 × (-2) × 3 × (-11) × (-5) = ?
Counting the number of negative integers in the product, we see that there are 3 negative integers: -2, -11, and -5. Next, we take the product of the absolute values of each number:
4 × |-2| × 3 × |-11| × |-5| = 1320.
Since there were an odd number of integers, the product is the opposite of 1320, which is -1320, so
4 × (-2) × 3 × (-11) × (-5) = -1320.
Dividing Integers
To divide a pair of integers if both integers have the same sign, divide the absolute value of the first integer by the absolute value of the second integer.
To divide a pair of integers if both integers have different signs, divide the absolute value of the first integer by the absolute value of the second integer, and give this result a negative sign.
Examples:
In the division below, both numbers are positive, so we just divide as usual.
4 ÷ 2 = 2.
In the division below, both numbers are negative, so we divide the absolute value of the first by the absolute value of the second.
(-24) ÷ (-3) = |-24| ÷ |-3| = 24 ÷ 3 = 8.
In the division (-100) ÷ 25, both number have different signs, so we divide the absolute value of the first number by the absolute value of the second, which is |-100| ÷ |25| = 100 ÷ 25 = 4, and give this result a negative sign: -4, so (-100) ÷ 25 = -4.
In the division 98 ÷ (-7), both number have different signs, so we divide the absolute value of the first number by the absolute value of the second, which is |98| ÷ |-7| = 98 ÷ 7 = 14, and give this result a negative sign: -14, so 98 ÷ (-7) = -14.
Integer coordinates
Integer coordinates are pairs of integers that are used to determine points in a grid, relative to a special point called the origin. The origin has coordinates (0,0). We can think of the origin as the center of the grid or the starting point for finding all other points. Any other point in the grid has a pair of coordinates (x,y). The x value or x-coordinate tells how many steps left or right the point is from the point (0,0), just like on the number line (negative is left of the origin, positive is right of the origin). The y value or y-coordinate tells how many steps up or down the point is from the point (0,0), (negative is down from the origin, positive is up from the origin). Using coordinates, we may give the location of any point in the grid we like by simply using a pair of numbers.
Example:
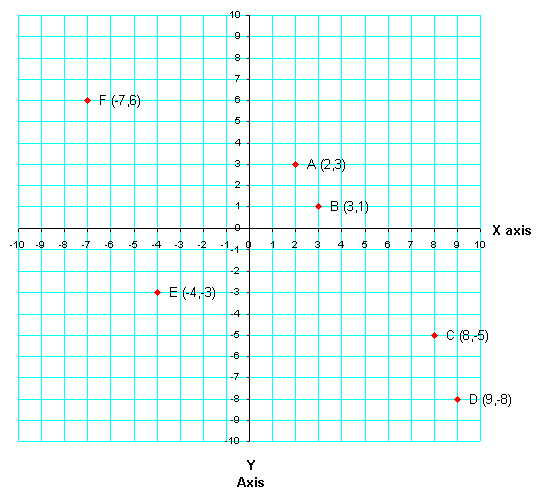
The origin below is where the x-axis and the y-axis meet. Point A has coordinates (2,3), since it is 2 units to the right and 3 units up from the origin. Point B has coordinates (3,1), since it is 3 units to the right, and 1 unit up from the origin. Point C has coordinates (8,-5), since it is 8 units to the right, and 5 units down from the origin. Point D has coordinates (9,-8); it is 9 units to the right, and 8 units down from the origin. Point E has coordinates (-4,-3); it is 4 units to the left, and 3 units down from the origin. Point F has coordinates (-7,6); it is 7 units to the left, and 6 units up from the origin.
Comparing Integers
We can compare two different integers by looking at their positions on the number line. For any two different places on the number line, the integer on the right is greater than the integer on the left. Note that every positive integer is greater than any negative integer.
Examples:
9 > 4, 6 > -9, -2 > -8, and 0 > -5
-2 < 1, 8 < 11, -7 < -5, and -10 < 0
- Details
- Parent Category: Math League Website
Percent Chances and probability A percent is a ratio of a number to 100. A percent can be expressed using the percent symbol %. Example: 10 percent or 10% are both the same, and stand for the ratio 10:100.Percent and Probability
What is a percent?
Percent as a fraction
Percent as a decimal
Estimating percents
Interest
Simple interest
Compound interest
Percent increase and decrease
Percent discount
What is an event?
Possible outcomes of an event
Probability
What is a Percent?
A percent is equivalent to a fraction with denominator 100. Example: 5% of something = 5/100 of that thing. Example: 2 1/2% is equal to what fraction? Example: 52% most nearly equals which one of 1/2, 1/4, 2, 8, or 1/5? Example: 13/25 is what %? Example: 8/200 is what %? Example: Write 80% as a fraction in lowest terms. Percent and hundredths are basically equivalent. This makes conversion between percent and decimals very easy. To convert from a decimal to a percent, just move the decimal 2 places to the right. For example, 0.15 = 15 hundredths = 15%. Example: 0.0006 = 0.06% Converting from percent to decimal form is similar, only you move the decimal point 2 places to the left. You must also be sure, before doing this, that the percentage itself is expressed in decimal form, without fractions. Example: Express 3% in decimal form. Moving the decimal 2 to the left (and adding in 0's to the left of the 3 as place holders,) we get 0.03. Example: Express 97 1/4% in decimal form. First we write 97 1/4 in decimal form: 97.25. Then we move the decimal 2 places to the left to get 0.9725, so 97 1/4% = 0.9725. This makes sense, since 97 1/4% is nearly 100%, and 0.9725 is nearly 1. When estimating percents, it is helpful to remember the fractional equivalent of some simple percents. 100% = 1 50% = 1/2 = 0.5 25% = 1/4 = 0.25 10% = 1/10 = 0.1 1% = 1/100 = 0.01 Because it is very easy to switch between a decimal and a percent, estimating a percent is as easy as estimating a fraction as a decimal, and converting to a percent by multiplying by 100. Example: Estimate 19 as a percent of 80. Example: Estimate 7 as a percent of 960. Example: Estimate 13% of 72. Example: Estimate 9.6% of 51. Method 2: We could estimate 10% of 51, which is just 5.1. This is not as close an estimate as method 1, but is still a good estimate of the actual answer of 4.896. Interest is a fee paid to borrow money. It is usually charged as a percent of the total amount borrowed. The percent charged is called the interest rate. The amount of money borrowed is called the principal. There are two types of interest, simple interest and compound interest. Example: A bank charges 7% interest on a $1000 loan. It will cost the borrower 7% of $1000, which is $70, for each year the money is borrowed. Note that when the loan is up, the borrower must pay back the original $1000. Simple interest is interest figured on the principal only, for the duration of the loan. Figure the interest on the loan for one year, and multiply this amount by the number of years the money is borrowed for. Example: A bank charges 8% simple interest on a $600 loan, which is to be paid back in two years. It will cost the borrower 8% of $600, which is $48, for each year the money is borrowed. Since it is borrowed for two years, the total charge for borrowing the money will be $96. After the two years the borrower will still have to pay back the original $600. Compound interest is interest figured on the principal and any interest owed from previous years. The interest charged the first year is just the interest rate times the amount of the loan. The interest charged the second year is the interest rate, times the sum of the loan and the interest from the first year. The interest charged the third year is the interest rate, times the sum of the loan and the first two years' interest amounts. Continue figuring the interest in this way for any additional years of the loan. Example: A bank charges 8% compound interest on a $600 loan, which is to be paid back in two years. It will cost the borrower 8% of $600 the first year, which is $48. The second year, it will cost 8% of $600 + $48 = $648, which is $51.84. The total amount of interest owed after the two years is $48 + $51.84 = $99.84. Note that this is more than the $96 that would be owed if the bank was charging simple interest. Example: A bank charges 4% compound interest on a $1000 loan, which is to be paid back in three years. It will cost the borrower 4% of $1000 the first year, which is $40. The second year, it will cost 4% of $1000 + $40 = $1040, which is $41.60. The third year, it will cost 4% of $1040 + $41.60 = $1081.60, which is $43.26 (with rounding). The total amount of interest owed after the three years is $40 + $41.60 + 43.26 = $124.86. Percent increase and decrease of a value measure how that value changes, as a percentage of its original value. Example: A collectors' comic book is worth $120 in 1994, and in 1995 its value is $132. The change is $132 - $120 = $12, an increase in price of $12; since $12 is 10% of $120, we say its value increased by 10% from 1994 to 1995. Example: A bakery makes a chocolate cake that has 8 grams of fat per slice. A new change in the recipe lowers the fat to 6 grams of fat per slice. The change is 8g - 6g = 2g, a decrease of 2 grams; since 2 grams is 25% of 8, we say that the new cake recipe has 25% less fat, or a 25% decrease in fat. Example: Amy is training for the 1500 meter run. When she started training she could run 1500 meters in 5 minutes and 50 seconds. After a year of practice her time decreased by 8%. How fast can she run the race now? Her old time was 5 × 60 + 50 = 350 seconds, and 8% of 350 is 28, so she can run the race in 350 - 28 = 322 seconds (5 minutes and 22 seconds). Example: A fishing magazine sells 110000 copies each month. The company's president wants to increase the sales by 6%. How many extra magazines would they have to sell to reach this goal? This problem is easy, since it only asks for the change in sales: 6% of 110000 equals 6600 more magazines. A discount is a decrease in price, so percent discount is the percent decrease in price. Example: Chocolate bars normally cost 80 cents each, but are on sale for 40 cents each, which is 50% of 80, so the chocolate is on sale at a 50% discount. Example: A compact disc that sells for $12 is on sale at a 20% discount. How much does the disc cost on sale? The amount of the discount is 20% of $12, which is $2.40, so the sale price is $12.00 - $2.40 = $9.60. Example: Movie tickets sell for $8.00 each, but if you buy 4 or more you get $1.00 off each ticket. What percent discount is this? We figure $1 as a percentage of $8: $1.00/$8.00 × 100% = 12.5%, so this is a 12.5% discount. An event is an experiment or collection of experiments. Examples: The following are examples of events. 1) A coin toss. Possible outcomes of an event are the results which may occur from any event. (Remember, they may not occur.) Examples: The following are possible outcomes of events. 1) A coin toss has two possible outcomes. The outcomes are "heads" and "tails".
Percent as a fraction
Answer:
2 1/2% = (2 1/2)/100 = 5/200 = 1/40
Answer: 52% = 52/100. This is very close to 50/100, or 1/2.
We want to convert 13/25 to a fraction with 100 in the denominator: 13/25 = (13 × 4)/(25 × 4) = 52/100, so 13/25 = 52%.
Alternatively, we could say: Let 13/25 be n%, and let us find n. Then 13/25 = n/100, so cross multiplying, 13 × 100 = 25 × n, so 25n = 13 × 100 = 1300. Then 25n ÷ 25 = 1300 ÷ 25, so n = 1300 ÷ 25 = 52. So 13/25 = n% = 52%.
Method 1: 8/200 = (4 × 2)/(100 × 2), so 8/200 = 4/100 = 4%.
Method 2: Let 8/200 be n%. Then 8/200 = n/100, so 200 × n = 800, and 200n ÷ 200 = 800 ÷ 200 = 4, so n% = 4%.
80% = 80/100, which is equal to 4/5 in lowest terms.
Percent as a decimal
Estimating percents
(100% of any number equals that number.)
(50% of any number equals half of that number.)
(25% of any number equals one-fourth of that number.)
(10% of any number equals one-tenth of that number.)
(1% of any number equals one-hundredth of that number.)
As a fraction, 19/80 20/80 = 1/4 =0.25 = 25%. The step used to estimate the percent occurred when we estimated 19/80 as 20/80.
20/80 = 1/4 =0.25 = 25%. The step used to estimate the percent occurred when we estimated 19/80 as 20/80.
The exact percent is actually 23.75%, so the estimate of 25% is only 1.25% off. (About 1 part in 100.)
As a fraction, 7/960  7/100 = 0.007 = 0.7%. The step used to estimate the percent occurred when we estimated 7/960 as 7/1000.
7/100 = 0.007 = 0.7%. The step used to estimate the percent occurred when we estimated 7/960 as 7/1000.
The exact percent, to the nearest thousandth of a percent, is actually 0.729%.
To estimate the percent of a number, we may convert the percent to a fraction, if useful, to estimate the percent.
Twice 13% is 26%, which is very close to 25%, and 25%=1/4. We may multiply both sides by 1/2 to get an estimate for 13%: 13% 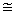 12.5% = 1/2 × 25% = 1/2 × 1/4 = 1/8. Using our estimate of 1/8 for 13%, 1/8 × 72 = 9, so we get an estimate of 9 for 13% of 72.
12.5% = 1/2 × 25% = 1/2 × 1/4 = 1/8. Using our estimate of 1/8 for 13%, 1/8 × 72 = 9, so we get an estimate of 9 for 13% of 72.
If we had calculated this exactly, 13% of 72 equals 9.36. It may look like we did a lot more work to get the estimate of 9 that just multiplying 72 by 0.13, but with practice, keeping in mind some simple percents and the fractions they are equal to will enable you to estimate some number combinations very quickly.
Method 1: We could estimate 9.6% of 50. It would be easy to estimate 9.6% of 100, which is just 9.6. Since 50 is half of 100, we can just take half of 9.6, which is 4.8. The actual value of 9.6% of 51 is 4.896, so an estimate of 4.8 is pretty good.
Interest
Simple Interest
Compound Interest
Percent increase and decrease
Percent Discount
What is an event?
2) Rolling a die.
3) Rolling 5 dice.
4) Drawing a card from a deck of cards.
5) Drawing 3 cards from a deck.
6) Drawing a marble from a bag of different colored marbles.
7) Spinning a spinner in a board game.
8) Tossing a coin and rolling a die.
Possible Outcomes of an Event
2) Rolling a regular six-sided die has six possible outcomes. You may get a side with 1, 2, 3, 4, 5, or 6 dots.
3) Drawing a card from a regular deck of 52 playing cards has 52 possible outcomes. Each of the 52 playing cards is different, so there are 52 possible outcomes for drawing a card.
4) How many different outcomes are there for the color of marble that may be drawn from a bag containing 3 red, 4 green, and 5 blue marbles? This event has 3 possible outcomes. You may get a red marble, a green marble, or a blue marble. Even if the marbles are different sizes, the outcome we are considering is the color of the marble that is drawn.
5) How many different outcomes are there for the colors of two marbles that may be drawn from a bag containing 3 red, 4 green, and 5 blue marble? This event has 6 possible outcomes: you may get two reds, two greens, two blues, a red and blue, a red and green, or a blue and green.
6) Rolling two regular dice, one of them red and one of them blue, has 36 possible outcomes. The outcomes are listed in the table below.
| Red Die | |||||||
| Result: | Red1 | Red2 | Red3 | Red4 | Red5 | Red6 | |
| Blue1 | Blue1, Red1 | Blue1, Red2 | Blue1, Red3 | Blue1, Red4 | Blue1, Red5 | Blue1, Red6 | |
| Blue2 | Blue2, Red1 | Blue2, Red2 | Blue2, Red3 | Blue2, Red4 | Blue2, Red5 | Blue2, Red6 | |
| Blue Die |
Blue3 | Blue3, Red1 | Blue3, Red2 | Blue3, Red3 | Blue3, Red4 | Blue3, Red5 | Blue3, Red6 |
| Blue4 | Blue4, Red1 | Blue4, Red2 | Blue4, Red3 | Blue4, Red4 | Blue4, Red5 | Blue4, Red6 | |
| Blue5 | Blue5, Red1 | Blue5, Red2 | Blue5, Red3 | Blue5, Red4 | Blue5, Red5 | Blue5, Red6 | |
| Blue6 | Blue6, Red1 | Blue6, Red2 | Blue6, Red3 | Blue6, Red4 | Blue6, Red5 | Blue6, Red6 | |
Note that the event tells us how to think of the outcomes. Even though there are 12 different marbles in example 4, the event tells us to count only the color of the die, so there are three outcomes. In example 6, the two dice are different, and there are 36 possible outcomes. Suppose we don't care about the color of the dice in example 6. Then we would only see 21 different outcomes: 1-1, 1-2, 1-3, 1-4, 1-5, 1-6, 2-2, 2-3, 2-4, 2-5, 2-6, 3-3, 3-4, 3-5, 3-6, 4-4, 4-5, 4-6, 5-5, 5-6, and 6-6. (We think of a 1 and a 2, a 1-2, as being the same as a 2 and a 1.) The probability of an outcome for a particular event is a number telling us how likely a particular outcome is to occur. This number is the ratio of the number of ways the outcome may occur to the number of total possible outcomes for the event. Probability is usually expressed as a fraction or decimal. Since the number of ways a certain outcome may occur is always smaller or equal to the total number of outcomes, the probability of an event is some number from 0 through 1. Example: Suppose there are 10 balls in a bucket numbered as follows: 1, 1, 2, 3, 4, 4, 4, 5, 6, and 6. A single ball is randomly chosen from the bucket. What is the probability of drawing a ball numbered 1? There are 2 ways to draw a 1, since there are two balls numbered 1. The total possible number of outcomes is 10, since there are 10 balls. The probability of drawing a 1 is the ratio 2/10 = 1/5. Example: Suppose there are 10 balls in a bucket numbered as follows: 1, 1, 2, 3, 4, 4, 4, 5, 6, and 6. A single ball is randomly chosen from the bucket. What is the probability of drawing a ball with a number greater than 4? There are 3 ways this may happen, since 3 of the balls are numbered greater than 4. The total possible number of outcomes is 10, since there are 10 balls. The probability of drawing a number greater than 4 is the ratio 3/10. Since this ratio is larger than the one in the previous example, we say that this event has a greater chance of occurring than drawing a 1. Example: Suppose there are 10 balls in a bucket numbered as follows: 1, 1, 2, 3, 4, 4, 4, 5, 6, and 6. A single ball is randomly chosen from the bucket. What is the probability of drawing a ball with a number greater than 6? Since none of the balls are numbered greater than 6, this can occur in 0 ways. The total possible number of outcomes is 10, since there are 10 balls. The probability of drawing a number greater than 6 is the ratio 0/10 = 0. Example: Suppose there are 10 balls in a bucket numbered as follows: 1, 1, 2, 3, 4, 4, 4, 5, 6, and 6. A single ball is randomly chosen from the bucket. What is the probability of drawing a ball with a number less than 7? Since all of the balls are numbered greater than 7, this can occur in 10 ways. The total possible number of outcomes is 10, since there are 10 balls. The probability of drawing a number less than 7 is the ratio 10/10 = 1. Example: Suppose a card is drawn at random from a regular deck of 52 cards. What is the probability that the card is an ace? There are 4 different ways that the card can be an ace, since 4 of the 52 cards are aces. There are 52 different total outcomes, one for each card in the deck. The probability of drawing an ace is the ratio 4/52 = 1/13. Example: Suppose a regular die is rolled. What is the probability of getting a 3 or a 6? There are a total of 6 possible outcomes. Rolling a 3 or a 6 are two of them, so the probability is the ratio of 2/6 = 1/3.
Probability of an Outcome
Note in the last two examples that a probability of 0 meant that the event would not occur, and a probability of 1 meant the event definitely would occur.
- Details
- Parent Category: Math League Website
Ratio and Proportion
Ratio
Comparing ratios
Proportion
Rate
Converting rates
Average rate of speed
Ratio
A ratio is a comparison of two numbers. We generally separate the two numbers in the ratio with a colon (:). Suppose we want to write the ratio of 8 and 12.
We can write this as 8:12 or as a fraction 8/12, and we say the ratio is eight to twelve.
Examples:
Jeannine has a bag with 3 videocassettes, 4 marbles, 7 books, and 1 orange.
1) What is the ratio of books to marbles?
Expressed as a fraction, with the numerator equal to the first quantity and the denominator equal to the second, the answer would be 7/4.
Two other ways of writing the ratio are 7 to 4, and 7:4.
2) What is the ratio of videocassettes to the total number of items in the bag?
There are 3 videocassettes, and 3 + 4 + 7 + 1 = 15 items total.
The answer can be expressed as 3/15, 3 to 15, or 3:15.
Comparing Ratios
To compare ratios, write them as fractions. The ratios are equal if they are equal when written as fractions.
Example:
Are the ratios 3 to 4 and 6:8 equal?
The ratios are equal if 3/4 = 6/8.
These are equal if their cross products are equal; that is, if 3 × 8 = 4 × 6. Since both of these products equal 24, the answer is yes, the ratios are equal.
Remember to be careful! Order matters!
A ratio of 1:7 is not the same as a ratio of 7:1.
Examples:
Are the ratios 7:1 and 4:81 equal? No!
7/1 > 1, but 4/81 < 1, so the ratios can't be equal.
Are 7:14 and 36:72 equal?
Notice that 7/14 and 36/72 are both equal to 1/2, so the two ratios are equal.
Proportion
A proportion is an equation with a ratio on each side. It is a statement that two ratios are equal.
3/4 = 6/8 is an example of a proportion.
When one of the four numbers in a proportion is unknown, cross products may be used to find the unknown number. This is called solving the proportion. Question marks or letters are frequently used in place of the unknown number.
Example:
Solve for n: 1/2 = n/4.
Using cross products we see that 2 × n = 1 × 4 =4, so 2 × n = 4. Dividing both sides by 2, n = 4 ÷ 2 so that n = 2.
Rate
A rate is a ratio that expresses how long it takes to do something, such as traveling a certain distance. To walk 3 kilometers in one hour is to walk at the rate of 3 km/h. The fraction expressing a rate has units of distance in the numerator and units of time in the denominator.
Problems involving rates typically involve setting two ratios equal to each other and solving for an unknown quantity, that is, solving a proportion.
Example:
Juan runs 4 km in 30 minutes. At that rate, how far could he run in 45 minutes?
Give the unknown quantity the name n. In this case, n is the number of km Juan could run in 45 minutes at the given rate. We know that running 4 km in 30 minutes is the same as running n km in 45 minutes; that is, the rates are the same. So we have the proportion
4km/30min = n km/45min, or 4/30 = n/45.
Finding the cross products and setting them equal, we get 30 × n = 4 × 45, or 30 × n = 180. Dividing both sides by 30, we find that n = 180 ÷ 30 = 6 and the answer is 6 km.
Converting rates
We compare rates just as we compare ratios, by cross multiplying. When comparing rates, always check to see which units of measurement are being used. For instance, 3 kilometers per hour is very different from 3 meters per hour!
3 kilometers/hour = 3 kilometers/hour × 1000 meters/1 kilometer = 3000 meters/hour
because 1 kilometer equals 1000 meters; we "cancel" the kilometers in converting to the units of meters.
Important:
One of the most useful tips in solving any math or science problem is to always write out the units when multiplying, dividing, or converting from one unit to another.
Example:
If Juan runs 4 km in 30 minutes, how many hours will it take him to run 1 km?
Be careful not to confuse the units of measurement. While Juan's rate of speed is given in terms of minutes, the question is posed in terms of hours. Only one of these units may be used in setting up a proportion. To convert to hours, multiply
4 km/30 minutes × 60 minutes/1 hour = 8 km/1 hour
Now, let n be the number of hours it takes Juan to run 1 km. Then running 8 km in 1 hour is the same as running 1 km in n hours. Solving the proportion,
8 km/1 hour = 1 km/n hours, we have 8 × n = 1, so n = 1/8.
Average Rate of Speed
The average rate of speed for a trip is the total distance traveled divided by the total time of the trip.
Example:
A dog walks 8 km at 4 km per hour, then chases a rabbit for 2 km at 20 km per hour. What is the dog's average rate of speed for the distance he traveled?
The total distance traveled is 8 + 2 = 10 km.
Now we must figure the total time he was traveling.
For the first part of the trip, he walked for 8 ÷ 4 = 2 hours. He chased the rabbit for 2 ÷ 20 = 0.1 hour. The total time for the trip is 2 + 0.1 = 2.1 hours.
The average rate of speed for his trip is 10/2.1 = 100/21 kilometers per hour.
- Details
- Parent Category: Math League Website
Space figures and basic solids
Space figures
Cross-section
Volume
Surface area
Cube
Cylinder
Sphere
Cone
Pyramid
Tetrahedron
Prism
Space Figure
A space figure or three-dimensional figure is a figure that has depth in addition to width and height. Everyday objects such as a tennis ball, a box, a bicycle, and a redwood tree are all examples of space figures. Some common simple space figures include cubes, spheres, cylinders, prisms, cones, and pyramids. A space figure having all flat faces is called a polyhedron. A cube and a pyramid are both polyhedrons; a sphere, cylinder, and cone are not.
Cross-Section
A cross-section of a space figure is the shape of a particular two-dimensional "slice" of a space figure.
Example:
The circle on the right is a cross-section of the cylinder on the left.
The triangle on the right is a cross-section of the cube on the left.

Volume
Volume is a measure of how much space a space figure takes up. Volume is used to measure a space figure just as area is used to measure a plane figure. The volume of a cube is the cube of the length of one of its sides. The volume of a box is the product of its length, width, and height.
Example:
What is the volume of a cube with side-length 6 cm?
The volume of a cube is the cube of its side-length, which is 63 = 216 cubic cm.
Example:
What is the volume of a box whose length is 4cm, width is 5 cm, and height is 6 cm?
The volume of a box is the product of its length, width, and height, which is 4 × 5 × 6 = 120 cubic cm.
Surface Area
The surface area of a space figure is the total area of all the faces of the figure.
Example:

What is the surface area of a box whose length is 8, width is 3, and height is 4? This box has 6 faces: two rectangular faces are 8 by 4, two rectangular faces are 4 by 3, and two rectangular faces are 8 by 3. Adding the areas of all these faces, we get the surface area of the box:
8 × 4 + 8 × 4 + 4 × 3 + 4 × 3 + 8 × 3 + 8 × 3 =
32 + 32 + 12 + 12 +24 + 24=
136.
Cube
A cube is a three-dimensional figure having six matching square sides. If L is the length of one of its sides, the volume of the cube is L3 = L × L × L. A cube has six square-shaped sides. The surface area of a cube is six times the area of one of these sides.
Example:
The space figure pictured below is a cube. The grayed lines are edges hidden from view.

Example:
What is the volume and surface are of a cube having a side-length of 2.1 cm?
Its volume would be 2.1 × 2.1 × 2.1 = 9.261 cubic centimeters.
Its surface area would be 6 × 2.1 × 2.1 = 26.46 square centimeters.
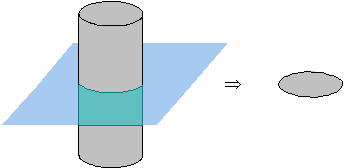
Cylinder
A cylinder is a space figure having two congruent circular bases that are parallel. If L is the length of a cylinder, and r is the radius of one of the bases of a cylinder, then the volume of the cylinder is L × pi × r2, and the surface area is 2 × r × pi × L + 2 × pi × r2.
Example:
The figure pictured below is a cylinder. The grayed lines are edges hidden from view.
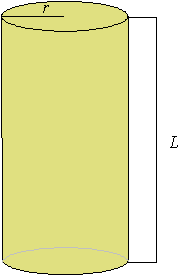
Sphere
A sphere is a space figure having all of its points the same distance from its center. The distance from the center to the surface of the sphere is called its radius. Any cross-section of a sphere is a circle.
If r is the radius of a sphere, the volume V of the sphere is given by the formula V = 4/3 × pi ×r3.
The surface area S of the sphere is given by the formula S = 4 × pi ×r2.
Example:
The space figure pictured below is a sphere.

Example:
To the nearest tenth, what is the volume and surface area of a sphere having a radius of 4cm?
Using an estimate of 3.14 for pi,
the volume would be 4/3 × 3.14 × 43 = 4/3 × 3.14 × 4 × 4 × 4 = 268 cubic centimeters.
Using an estimate of 3.14 for pi, the surface area would be 4 × 3.14 × 42 = 4 × 3.14 × 4 × 4 = 201 square centimeters.
Cone
A cone is a space figure having a circular base and a single vertex.
If r is the radius of the circular base, and h is the height of the cone, then the volume of the cone is 1/3 × pi × r2 × h.
Example:
What is the volume in cubic cm of a cone whose base has a radius of 3 cm, and whose height is 6 cm, to the nearest tenth?
We will use an estimate of 3.14 for pi.
The volume is 1/3 × pi × 32 × 6 = pi ×18 = 56.52, which equals 56.5 cubic cm when rounded to the nearest tenth.
Example:
The pictures below are two different views of a cone.


Pyramid
A pyramid is a space figure with a square base and 4 triangle-shaped sides.
Example:
The picture below is a pyramid. The grayed lines are edges hidden from view.
Tetrahedron
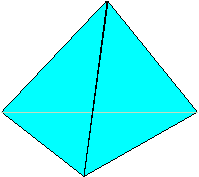
A tetrahedron is a 4-sided space figure. Each face of a tetrahedron is a triangle.
Example:
The picture below is a tetrahedron. The grayed lines are edges hidden from view.
Prism
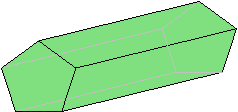
A prism is a space figure with two congruent, parallel bases that are polygons.
Examples:
The figure below is a pentagonal prism (the bases are pentagons). The grayed lines are edges hidden from view.
The figure below is a triangular prism (the bases are triangles). The grayed lines are edges hidden from view.
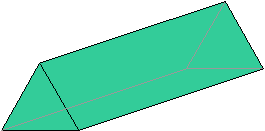
The figure below is a hexagonal prism (the bases are hexagons). The grayed lines are edges hidden from view..

- Details
- Parent Category: Math League Website
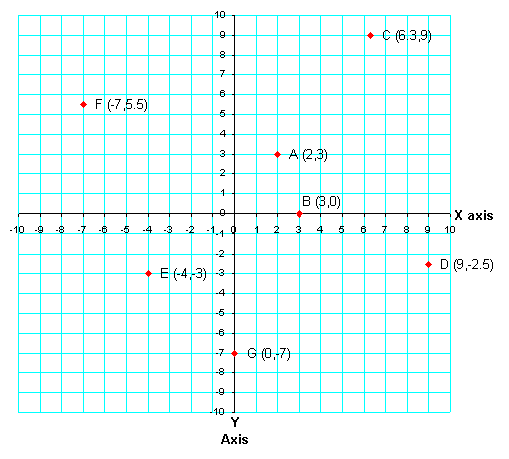
What is a coordinate? Coordinates are pairs of numbers that are used to determine points in a plane, relative to a special point called the origin. The origin has coordinates (0,0). We can think of the origin as the center of the plane or the starting point for finding all other points. Any other point in the plane has a pair of coordinates (x,y). The x value or x-coordinate tells how far left or right the point is from the point (0,0), just like on the number line (negative is left of the origin, positive is right of the origin). The y value or y-coordinate tells how far up or down the point is from the point (0,0), (negative is down from the origin, positive is up from the origin). Using coordinates, we may give the location of any point we like by simply using a pair of numbers. Example: The origin below is where the x-axis and the y-axis meet. Point A has coordinates (2,3), since it is 2 units to the right and 3 units up from the origin. Point B has coordinates (3,0), since it is 3 units to the right, and lies on the x-axis. Point C has coordinates (6.3,9), since it is 6.3 units to the right, and 9 units up from the origin. Point D has coordinates (9,-2.5); it is 9 units to the right, and 2.5 units down from the origin. Point E has coordinates (-4,-3); it is 4 units to the left, and 3 units down from the origin. Point F has coordinates (-7,5.5); it is 7 units to the left, and 6 units up from the origin. Point G has coordinates (0,-7) since it lies on the y-axis 7 units below the origin.Coordinates and similar figures
Similar figures
Congruent figures
Rotation
Reflection
Folding
Symmetric figure
What is a Coordinate?
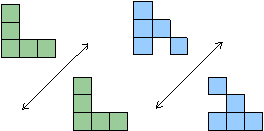
Figures that have the same shape are called similar figures. They may be different sizes or turned somewhat. Example: The following pairs of figures are similar.
Similar Figures
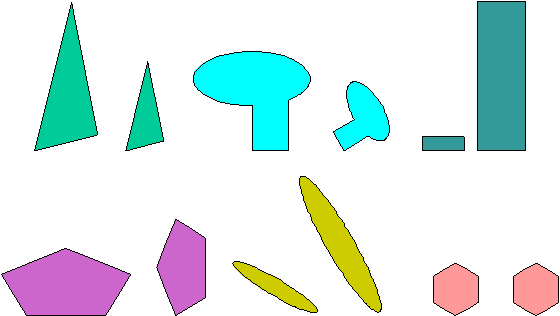
These pairs of figures are not similar.

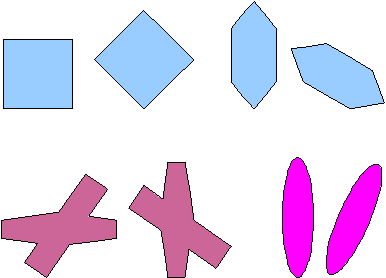
Two figures are congruent if they have the same shape and size. Example: The following pairs of figures below are congruent. Note that if two figures are congruent, they must be similar.
Congruent Figures
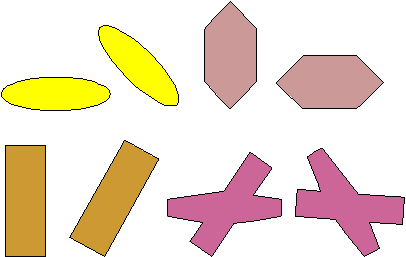
The pairs below are similar but not congruent.
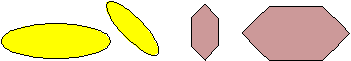
The pairs below are not similar or congruent.

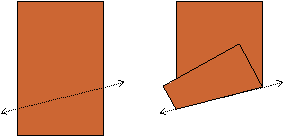
When a figure is turned, we call it a rotation of the figure. We can measure this rotation in terms of degrees; a 360 degree turn rotates a figure around once back to its original position. Example: For the following pairs of figures, the figure on the right is a rotation of the figure on the left.
Rotation
If we flip (or mirror) along some line, we say the figure is a reflection along that line. Examples: Reflections along a vertical line:
Reflection
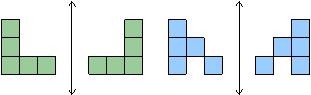
Reflections along a horizontal line:

Reflections along a diagonal line:
When we talk about folding a plane figure, we mean folding it as if it were a piece of paper in that shape. We might fold this into a solid figure such as a box, or fold the figure flat along itself. Example: Folding the figure on the left into a box:
Folding
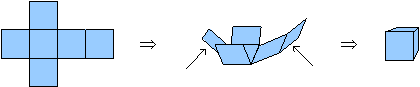
Folding the figure on the left flat along the dotted line:
A figure that can be folded flat along a line so that the two halves match perfectly is a symmetric figure; such a line is called a line of symmetry. Examples:
Symmetric Figure
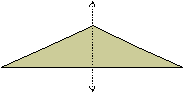
The triangle below is a symmetric figure. The dotted line is the line of symmetry.
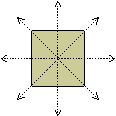
The square below is a symmetric figure. It has four different lines of symmetry shown below.
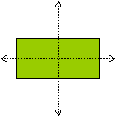
The rectangle below is a symmetric figure. It has two different lines of symmetry shown below.
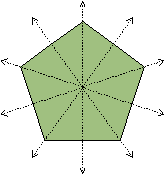
The regular pentagon below is a symmetric figure. It has five different lines of symmetry shown below.
The circle below is a symmetric figure. Any line that passes through its center is a line of symmetry!

The figures shown below are not symmetric.
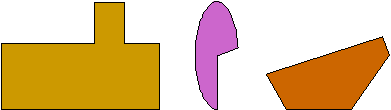
- Details
- Parent Category: Math League Website
The area of a figure measures the size of the region enclosed by the figure. This is usually expressed in terms of some square unit. A few examples of the units used are square meters, square centimeters, square inches, or square kilometers. Area and perimeter
Area
Area of a square
Area of a rectangle
Area of a parallelogram
Area of a trapezoid
Area of a triangle
Area of a circle
Perimeter
Circumference of a circle
Area
If l is the side-length of a square, the area of the square is l2 or l × l. Example: What is the area of a square having side-length 3.4? The area of a rectangle is the product of its width and length. Example: What is the area of a rectangle having a length of 6 and a width of 2.2? The area of a parallelogram is b × h, where b is the length of the base of the parallelogram, and h is the corresponding height. To picture this, consider the parallelogram below:
Area of a Square
The area is the square of the side-length, which is 3.4 × 3.4 = 11.56.
Area of a Rectangle
The area is the product of these two side-lengths, which is 6 × 2.2 = 13.2.
Area of a Parallelogram
We can picture "cutting off" a triangle from one side and "pasting" it onto the other side to form a rectangle with side-lengths b and h. This rectangle has area b × h.

Example: What is the area of a parallelogram having a base of 20 and a corresponding height of 7?
The area is the product of a base and its corresponding height, which is 20 × 7 = 140.
Area of a Trapezoid
If a and b are the lengths of the two parallel bases of a trapezoid, and h is its height, the area of the trapezoid is To picture this, consider two identical trapezoids, and "turn" one around and "paste" it to the other along one side as pictured below:
1/2 × h × (a + b) .
The figure formed is a parallelogram having an area of h × (a + b), which is twice the area of one of the trapezoids. Example: What is the area of a trapezoid having bases 12 and 8 and a height of 5? Consider a triangle with base length b and height h. To picture this, we could take a second triangle identical to the first, then rotate it and "paste" it to the first triangle as pictured below: The figure formed is a parallelogram with base length b and height h, and has area b × ×h. Example: What is the area of the triangle below having a base of length 5.2 and a height of 4.2?
Using the formula for the area of a trapezoid, we see that the area is
1/2 × 5 × (12 + 8) = 1/2 × 5 × 20 = 1/2 × 100 = 50.
Area of a Triangle
or
The area of the triangle is 1/2 × b × h. or
This area is twice that of the triangle, so the triangle has area 1/2 × b × h.
The area of a triangle is half the product of its base and height, which is 1/2 ×5.2 × 4.2 = 2.6 × 4.2 = 10.92..
The area of a circle is Pi × r2 or Pi × r × r, where r is the length of its radius. Pi is a number that is approximately 3.14159. Example: What is the area of a circle having a radius of 4.2 cm, to the nearest tenth of a square cm? Using an approximation of 3.14159 for Pi, and the fact that the area of a circle is Pi × r2, the area of this circle is Pi × 4.22 The perimeter of a polygon is the sum of the lengths of all its sides. Example: What is the perimeter of a rectangle having side-lengths of 3.4 cm and 8.2 cm? Since a rectangle has 4 sides, and the opposite sides of a rectangle have the same length, a rectangle has 2 sides of length 3.4 cm, and 2 sides of length 8.2 cm. The sum of the lengths of all the sides of the rectangle is 3.4 + 3.4 + 8.2 + 8.2 = 23.2 cm. Example: What is the perimeter of a square having side-length 74 cm? Since a square has 4 sides of equal length, the perimeter of the square is 74 + 74 + 74 + 74 = 4 × 74 = 296. Example: What is the perimeter of a regular hexagon having side-length 2.5 m? A hexagon is a figure having 6 sides, and since this is a regular hexagon, each side has the same length, so the perimeter of the hexagon is 2.5 + 2.5 + 2.5 + 2.5 + 2.5 + 2.5 = 6 × 2.5 = 15m. Example: What is the perimeter of a trapezoid having side-lengths 10 cm, 7 cm, 6 cm, and 7 cm? The perimeter is the sum 10 + 7 + 6 + 7 = 30cm. The distance around a circle. It is equal to Pi ( Example: What is the circumference of a circle having a diameter of 7.9 cm, to the nearest tenth of a cm? Using an approximation of 3.14159 for
Area of a Circle
 3.14159 × 4.22 =55.41…square cm, which is 55.4 square cm when rounded to the nearest tenth.
3.14159 × 4.22 =55.41…square cm, which is 55.4 square cm when rounded to the nearest tenth.
Perimeter
Circumference of a Circle
) times the diameter of the circle. Pi or
is a number that is approximately 3.14159.
, and the fact that the circumference of a circle is
times the diameter of the circle, the circumference of the circle is Pi × 7.9
 3.14159 × 7.9 = 24.81…cm, which equals 24.8 cm when rounded to the nearest tenth of a cm.
3.14159 × 7.9 = 24.81…cm, which equals 24.8 cm when rounded to the nearest tenth of a cm.




