Fractions
- Details
- Parent Category: Math League Website
- Published: 15 September 2008
Prime numbers A whole number greater than one that is divisible by only 1 and itself. The numbers 2, 3, 5, 37, and 101 are some examples of prime numbers. The greatest common factor of two or more whole numbers is the largest whole number that divides each of the numbers. There are two methods of finding the greatest common factor of two numbers. Method 1: List all the factors of each number, then list the common factors and choose the largest one. Example: 36: 1, 2, 3, 4, 6, 9, 12, 18, 36 54: 1, 2, 3, 6, 9, 18, 27, 54 The common factors are: 1, 2, 3, 6, 9, and 18. The greatest common factor is: 18. Method 2: List the prime factors, then multiply the common prime factors. Example: 36 = 2 × 2 × 3 × 3 54 = 2 × 3 × 3 × 3 The common prime factors are 2, 3, and 3. The greatest common factor is 2 × 3 × 3 = 18.. The least common multiple of two or more nonzero whole numbers is the smallest whole number that is divisible by each of the numbers. There are two common methods for finding the least common multiple of 2 numbers. Method 1: List the multiples of each number, and look for the smallest number that appears in each list. Example: Find the least common multiple of 12 and 42. We list the multiples of each number: 12: 12, 24, 36, 48, 60, 72, 84, ... 42: 42, 84, 126, 168, 190, ... We see that the number 84 is the smallest number that appears in each list. Method 2: Factor each of the numbers into primes. For each different prime number in either of the factorizations, follow these steps: 1. Count the number of times it appears in each of the factorizations. 2. Take the largest of these two counts. 3. Write down that prime number as many times as the count in step 2. To find the least common multiple take the product of all of the prime numbers written down in steps 1, 2, and 3. Example: Find the least common multiple of 24 and 90. First, we find the prime factorization of each number. 24 = 2 × 2 × 2 × 3 90 = 2 × 3 × 3 × 5 The prime numbers 2, 3, and 5 appear in the factorizations. We follow steps 1 through 3 for each of these primes. The number 2 occurs 3 times in the first factorization and 1 time in the second, so we will use three 2's. The number 3 occurs 1 time in the first factorization and 2 times in the second, so we will use two 3's. The number 5 occurs 0 times in the first factorization and 1 time in the second factorization, so we will use one 5. The least common multiple is the product of three 2's, two 3's, and one 5. 2 × 2 × 2 × 3 × 3 × 5 = 360 Example: Find the least common multiple of 14 and 49. First, we find the prime factorization of each number. 14 = 2 × 7 49 = 7 × 7 The prime numbers 2 and 7 appear in the factorizations. We follow steps 1 through 3 for each of these primes. The number 2 occurs 1 times in the first factorization and 0 times in the second, so we will use one 2. The number 7 occurs 1 time in the first factorization and 2 times in the second, so we will use two 7's. The least common multiple is the product of one 2 and two 7's. 2 × 7 × 7 = 98 Examples: Some other least common multiples are listed below. The least common multiple of 12 and 9 is 36. The least common multiple of 6 and 18 is 18. The least common multiple of 2, 3, 4, and 5 is 60. A fraction is a number that expresses part of a group. Fractions are written in the form The number a is called the numerator, and the number b is called the denominator. Examples: The following numbers are all fractions Example: The fraction 4/6 represents the shaded portion of the circle below. There are 6 pieces in the group, and 4 of them are shaded.Fractions
Greatest common factor
Least common multiple
What is a fraction?
Equivalent fractions
Comparing fractions
Converting and reducing fractions
Lowest terms
Improper fractions
Mixed numbers
Converting mixed numbers to improper fractions
Converting improper fractions to mixed numbers
Writing a fraction as a decimal
Rounding a fraction to the nearest hundredth
Adding and subtracting fractions
Adding and subtracting mixed numbers
Multiplying fractions and whole numbers
Multiplying fractions and fractions
Multiplying mixed numbers
Reciprocal
Dividing fractions
Dividing mixed numbers
Simplifying complex fractions
Repeating decimals
Prime Numbers
Greatest Common Factor
Least Common Multiple
What is a Fraction?
or a/b, where a and b are whole numbers, and the number b is not 0. For the purposes of these web pages, we will denote fractions using the notation a/b, though the preferred notation is generally
.
1/2, 3/7, 6/10, 4/99

Example: The fraction 3/8 represents the shaded portion of the circle below. There are 8 pieces in the group, and 3 of them are shaded.
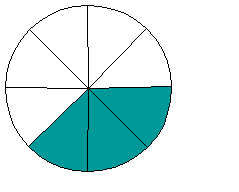
Example: The fraction 2/3 represents the shaded portion of the circle below. There are 3 pieces in the group, and 2 of them are shaded.

Equivalent fractions are different fractions which name the same amount. Examples: The fractions 1/2, 2/4, 3/6, 100/200, and 521/1042 are all equivalent fractions. Example: Test if 3/7 and 18/42 are equivalent fractions. Example: Test if 2/4 and 13/20 are equivalent fractions. 1. To compare fractions with the same denominator, look at their numerators. The larger fraction is the one with the larger numerator. Example: Compare the fractions 3/7 and 1/2. Example: Compare the fractions 13/20 and 3/5. For any fraction, multiplying the numerator and denominator by the same nonzero number gives an equivalent fraction. We can convert one fraction to an equivalent fraction by using this method. Examples: 1/2 = (1 × 3)/(2 × 3) = 3/6 2/3 = (2 × 2)/(3 × 2) = 4/6 3/5 = (3 × 4)/(5 × 4) = 12/20 Another method of converting one fraction to an equivalent fraction is by dividing the numerator and denominator by a common factor of the numerator and denominator. Examples: 20/42 = (20 ÷ 2)/(42 ÷ 2) = 10/21 36/72 = (36 ÷ 3)/(72 ÷ 3) = 12/24 9/27 = (9 ÷ 3)/(27 ÷ 3) = 3/9 When we divide the numerator and denominator of a fraction by their greatest common factor, the resulting fraction is an equivalent fraction in lowest terms. A fraction is in lowest terms when the greatest common factor of its numerator and denominator is 1. There are two methods of reducing a fraction to lowest terms. Method 1: Divide the numerator and denominator by their greatest common factor. 12/30 = (12 ÷ 6)/(30 ÷ 6) = 2/5 Method 2: Divide the numerator and denominator by any common factor. Keep dividing until there are no more common factors. 12/30 = (12 ÷ 2)/(30 ÷ 2) = 6/15 = (6 ÷ 3)/(15 ÷ 3) = 2/5 Improper fractions have numerators that are larger than or equal to their denominators. Examples: 11/4, 5/5, and 13/2 are improper fractions. Mixed numbers have a whole number part and a fraction part. Examples: To change a mixed number into an improper fraction, multiply the whole number by the denominator and add it to the numerator of the fractional part. Examples: 2 3/4 = ((2 × 4) + 3)/4 =11/4 6 1/2 = ((6 × 2) + 1)/2 = 13/2 To change an improper fraction into a mixed number, divide the numerator by the denominator. The remainder is the numerator of the fractional part. Examples: 11/4 = 11 ÷ 4 = 2 r3 = 2 3/4 13/2 = 13 ÷ 2 = 6 r1 = 6 1/2 Method 1 - Convert to an equivalent fraction whose denominator is a power of 10, such as 10, 100, 1000, 10000, and so on, then write in decimal form. Examples: 1/4 = (1 × 25)/(4 × 25) = 25/100 = 0.25 3/20 = (3 × 5)/(20 × 5) = 15/100 = 0.15 9/8 = (9 × 125)/(8 × 125) = 1125/1000 = 1.125 Method 2 - Divide the numerator by the denominator. Round to the decimal place asked for, if necessary. Example: 13/4 = 13 ÷ 4 = 3.25 Example: Convert 3/7 to a decimal. Round to the nearest thousandth. We divide one decimal place past the place we need to round to, then round the result. 3/7 = 3 ÷ 7 = 0.4285… which equals 0.429 when rounded to the nearest thousandth. Example: Convert 4/9 to a decimal. Round to the nearest hundredth. We divide one decimal place past the place we need to round to, then round the result. 4/9 = 4 ÷ 9 = 0.4444… which equals 0.44 when rounded to the nearest hundredth. Divide to the thousandths place. If the last digit is less than 5, drop it. This is particularly useful for converting a fraction to a percent, if we want to convert to the nearest percent. 1/3 = 1 ÷ 3 = 0.333… which rounds to 0.33 If the last digit is 5 or greater, drop it and round up. 2/7 = 2 ÷ 7 = 0.285 which rounds to 0.29 If the fractions have the same denominator, their sum is the sum of the numerators over the denominator. If the fractions have the same denominator, their difference is the difference of the numerators over the denominator. We do not add or subtract the denominators! Reduce if necessary. Examples: 3/8 + 2/8 = 5/8 9/2 - 5/2 = 4/2 = 2 If the fractions have different denominators: Example: 3/4 + 1/6 = ? The least common denominator is 12. 3/4 + 1/6 = 9/12 + 2/12 = 11/12. Example: 9/10 - 1/2 = ? The least common denominator is 10. 9/10 - 1/2 = 9/10 - 5/10 = 4/10 = 2/5. Example: 2/3 + 2/7 = ? The least common denominator is 21 2/3 + 2/7 = 14/21 + 6/21 = 20/21. To add or subtract mixed numbers, simply convert the mixed numbers into improper fractions, then add or subtract them as fractions. Example: 9 1/2 + 5 3/4 = ? Converting each number to an improper fraction, we have 9 1/2 = 19/2 and 5 3/4 = 23/4. We want to calculate 19/2 + 23/4. The LCM of 2 and 4 is 4, so 19/2 + 23/4 = 38/4 + 23/4 = (38 + 23)/4 = 61/4. Converting back to a mixed number, we have 61/4 = 15 1/4. The strategy of converting numbers into fractions when adding or subtracting is often useful, even in situations where one of the numbers is whole or a fraction. Example: 13 - 1 1/3 = ? In this situation, we may regard 13 as a mixed number without a fractional part. To convert it into a fraction, we look at the denominator of the fraction 4/3, which is 1 1/3 expressed as an improper fraction. The denominator is 3, and 13 = 39/3. So 13 - 1 1/3 = 39/3 - 4/3 = (39-4)/3 = 35/3, and 35/3 = 11 2/3. Example: 5 1/8 - 2/3 = ? This time, we may regard 2/3 as a mixed number with 0 as its whole part. Converting the first mixed number to an improper fraction, we have 5 1/8 = 41/8. The problem becomes 5 1/8 - 2/3 = 41/8 - 2/3 = 123/24 - 16/24 = (123 - 16)/24 = 107/24. Converting back to a mixed number, we have 107/24 = 4 11/24. Example: 92 + 4/5 = ? This is easy. To express this as a mixed number, just put the whole number and the fraction side by side. The answer is 92 4/5. To multiply a fraction by a whole number, write the whole number as an improper fraction with a denominator of 1, then multiply as fractions. Example: 8 × 5/21 = ? We can write the number 8 as 8/1. Now we multiply the fractions. 8 × 5/21 = 8/1 × 5/21 = (8 × 5)/(1 × 21) = 40/21 Example: 2/15 × 10 = ? We can write the number 10 as 10/1. Now we multiply the fractions. 2/15 × 10 = 2/15 × 10/1 = (2 × 10)/(15 × 1) = 20/15 = 4/3 When two fractions are multiplied, the result is a fraction with a numerator that is the product of the fractions' numerators and a denominator that is the product of the fractions' denominators. Example: 4/7 × 5/11 = ? The numerator will be the product of the numerators: 4 × 5, and the denominator will be the product of the denominators: 7 × 11. The answer is (4 × 5)/(7 × 11) = 20/77. Remember that like numbers in the numerator and denominator cancel out. Example: 14/15 × 15/17 = ? Since the 15's in the numerator and denominator cancel, the answer is 14/15 × 15/17 = 14/1 × 1/17 = (14 × 1)/(1 × 17) = 14/17 Example: 4/11 × 22/36 = ? In the solution below, first we cancel the common factor of 11 in the top and bottom of the product, then we cancel the common factor of 4 in the top and bottom of the product. 4/11 × 22/36 = 4/1 × 2/36 = 1/1 × 2/9 = 2/9 To multiply mixed numbers, convert them to improper fractions and multiply. Example: 4 1/5 × 2 2/3 = ?. Converting to improper fractions, we get 4 1/5 = 21/5 and 2 2/3 = 8/3. So the answer is 4 1/5 × 2 2/3 = 21/5 × 8/3 = (21 × 8)/(5 × 3) = 168/15 = 11 3/15. Examples: 3/4 × 1 1/8 = 3/4 × 9/8 = 27/32. 3 × 7 3/4 = 3 × 31/4 = (3 × 31)/4 = 93/4 = 23 1/4. The reciprocal of a fraction is obtained by switching its numerator and denominator. To find the reciprocal of a mixed number, first convert the mixed number to an improper fraction, then switch the numerator and denominator of the improper fraction. Notice that when you multiply a fraction and its reciprocal, the product is always 1. Example: Find the reciprocal of 31/75. We switch the numerator and denominator to find the reciprocal: 75/31. Example: Find the reciprocal of 12 1/2. First, convert the mixed number to an improper fraction: 12 1/2 = 25/2. Next, we switch the numerator and denominator to find the reciprocal: 2/25. To divide a number by a fraction, multiply the number by the reciprocal of the fraction. Examples: 7 ÷ 1/5 = 7 × 5/1 = 7 × 5 = 35 1/5 ÷ 16 = 1/5 ÷ 16/1 = 1/5 × 1/16 = (1 × 1)/(5 × 16) = 1/80 3/5 ÷ 7/12 = 3/5 × 12/7 = (3 × 12)/(5 × 7) = 36/35 or 1 1/35
Equivalent Fractions
The fractions 3/7, 6/14, and 24/56 are all equivalent fractions.
We can test if two fractions are equivalent by cross-multiplying their numerators and denominators. This is also called taking the cross-product.
The first cross-product is the product of the first numerator and the second denominator: 3 × 42 = 126.
The second cross-product is the product of the second numerator and the first denominator: 18 × 7 = 126.
Since the cross-products are the same, the fractions are equivalent.
The first cross-product is the product of the first numerator and the second denominator: 2 × 20 = 40.
The second cross-product is the product of the second numerator and the first denominator: 4 × 13 = 52.
Since the cross-products are different, the fractions are not equivalent. Since the second cross-product is larger than the first, the second fraction is larger than the first.
Comparing Fractions
2. To compare fractions with different denominators, take the cross product. The first cross-product is the product of the first numerator and the second denominator. The second cross-product is the product of the second numerator and the first denominator. Compare the cross products using the following rules:
a. If the cross-products are equal, the fractions are equivalent.
b. If the first cross product is larger, the first fraction is larger.
c. If the second cross product is larger, the second fraction is larger.
The first cross-product is the product of the first numerator and the second denominator: 3 × 2 = 6.
The second cross-product is the product of the second numerator and the first denominator: 7 × 1 = 7.
Since the second cross-product is larger, the second fraction is larger.
The first cross-product is the product of the first numerator and the second denominator: 5 × 13 = 65.
The second cross-product is the product of the second numerator and the first denominator: 20 × 3 = 60.
Since the first cross-product is larger, the first fraction is larger.
Converting and Reducing Fractions
Lowest Terms
Improper Fractions
Mixed Numbers
are mixed numbers also written as 2 3/4 and 6 1/2. In these web pages, we denote mixed numbers in the form a b/c.
Converting Mixed Numbers to Improper Fractions
Converting Improper Fractions to Mixed Numbers
Writing a Fraction as a Decimal
Rounding a Fraction to the Nearest Hundredth
Adding and Subtracting Fractions
1) First, find the least common denominator.
2) Then write equivalent fractions using this denominator.
3) Add or subtract the fractions. Reduce if necessary.
Adding and Subtracting Mixed Numbers
Multiplying Fractions and Whole Numbers
Multiplying Fractions and Fractions
Multiplying Mixed Numbers
Reciprocal
Dividing Fractions
Dividing Mixed Numbers
To divide mixed numbers, you should always convert to improper fractions, then multiply the first number by the reciprocal of the second. Examples: 1 1/2 ÷ 3 1/8 = 3/2 ÷ 25/8 = 3/2 × 8/25 = (3 × 8)/(2 × 25) = 24/50 1 ÷ 3 3/5 = 1/1 ÷ 18/5 = 1/1 × 5/18 = (1 × 5)/(1 × 18) = 5/18 3 1/8 ÷ 2 = 25/8 ÷ 2/1 = 25/8 × 1/2 = (25 × 1)/(8 × 2) = 25/16 or 1 9/16. A complex fraction is a fraction whose numerator or denominator is also a fraction or mixed number. Example of complex fractions:
Simplifying Complex Fractions
otherwise written as (1/4)/(2/3), (3/7)/100, 11/(2/3), and (23 1/5)/(2/3). To simplify complex fractions, change the complex fraction into a division problem: divide the numerator by the denominator. The first of these examples becomes (1/4)/(2/3) = 1/4 ÷ 2/3 = 1/4 × 3/2 = 3/8. The second of these becomes (3/7)/100 = 3/7 ÷ 100 = 3/7 × 1/100 = 3/700. The third of these becomes 11/(2/3) = 11 ÷ 2/3 = 11 × 3/2 = 33/2 = 16 1/2. The fourth of these becomes (23 1/5)/(2/3) = 23 1/5 ÷ 2/3 = 116/5 ÷ 2/3 = 116/5 × 3/2 = 174/5 = 34 4/5.
Repeating Decimals
Every fraction can be written as a decimal. For example, 1/3 is 1 divided by 3. If you use a calculator to find 1 ÷ 3, the calculator returns 0.333333... This is called a repeating decimal. To represent the idea that the 3's repeat forever, one uses a horizontal bar (overstrike) as shown below:
Example: What is the repeating decimal for 1/7 ? Dividing 7 into 1, we get 0.142857142..., and we see the pattern begin to repeat with the second 1, so .




