Basic Terms

Basic terms

Lines
Points
Intersection
Line segments
Rays
Endpoints
Parallel lines

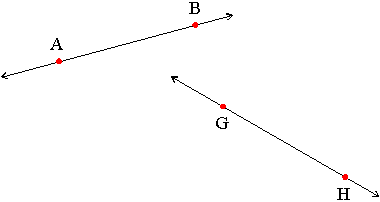
Lines

A line is one of the basic terms in geometry. We may think of a line as a "straight" line that we might draw with a ruler on a piece of paper, except that in geometry, a line extends forever in both directions. We write the name of a line passing through two different points A and B as "line AB" or as , the two-headed arrow over AB signifying a line passing through points A and B.

Example: The following is a diagram of two lines: line AB and line HG.

The arrows signify that the lines drawn extend indefinitely in each direction.

Points

A point is one of the basic terms in geometry. We may think of a point as a "dot" on a piece of paper. We identify this point with a number or letter. A point has no length or width, it just specifies an exact location.

Example: The following is a diagram of points A, B, C, and Q:

Intersection

The term intersect is used when lines, rays, line segments or figures meet, that is, they share a common point. The point they share is called the point of intersection. We say that these figures intersect.

Example: In the diagram below, line AB and line GH intersect at point D:

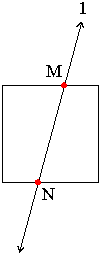
Example: In the diagram below, line 1 intersects the square in points M and N:

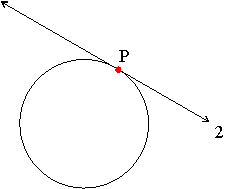
Example: In the diagram below, line 2 intersects the circle at point P:

Line Segments

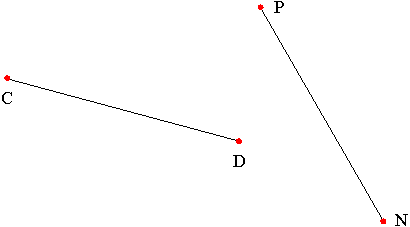
A line segment is one of the basic terms in geometry. We may think of a line segment as a "straight" line that we might draw with a ruler on a piece of paper. A line segment does not extend forever, but has two distinct endpoints. We write the name of a line segment with endpoints A and B as "line segment AB" or as . Note how there are no arrow heads on the line over AB such as when we denote a line or a ray.

Example: The following is a diagram of two line segments: line segment CD and line segment PN, or simply segment CD and segment PN.

Rays

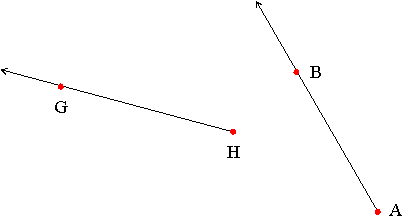
A ray is one of the basic terms in geometry. We may think of a ray as a "straight" line that begins at a certain point and extends forever in one direction. The point where the ray begins is known as its endpoint. We write the name of a ray with endpoint A and passing through a point B as "ray AB" or as . Note how the arrow heads denotes the direction the ray extends in: there is no arrow head over the endpoint.

Example: The following is a diagram of two rays: ray HG and ray AB.

Endpoints

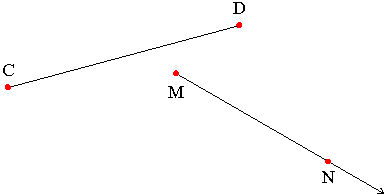
An endpoint is a point used to define a line segment or ray. A line segment has two endpoints; a ray has one.

Example: The endpoints of line segment DC below are points D and C, and the endpoint of ray MN is point M below:

Parallel Lines

Two lines in the same plane which never intersect are called parallel lines. We say that two line segments are parallel if the lines that they lie on are parallel. If line 1 is parallel to line 2, we write this as

line 1 || line 2

When two line segments DC and AB lie on parallel lines, we write this as

segment DC || segment AB.

Example: Lines 1 and 2 below are parallel.

Example: The opposite sides of the rectangle below are parallel. The lines passing through them never meet.